在数学的天空中，闪耀着无数璀璨的星辰，而其中最为耀眼的一颗，非格奥尔格·弗里德里希·伯纳德·黎曼（Georg Friedrich Bernhard Riemann）莫属。黎曼是19世纪的德国数学家，他在数学的诸多领域里做出了深远的贡献，其中最具影响力的便是他提出的黎曼几何。

1826年，黎曼出生在德国的一个贫穷的牧师家庭。他的数学天赋在很小的时候就已经显现出来，但他的父亲却希望他能成为一名牧师，因此他早年的教育并不是以数学为主。然而，命运却赐予他一次机会，他的家庭教师注意到了他在数学方面的才能，开始引导他进行数学的学习。他的数学才能得以充分发展，这让他在1846年得以进入哥廷根大学进行数学的深造。

黎曼的数学才华很快得到了当时的数学巨擘高斯（Gauss）的赏识，他在高斯的指导下进行研究，并于1851年获得了博士学位。在他的博士论文中，黎曼首次提出了黎曼几何的概念，这在当时的数学界引起了轩然大波，被誉为数学史上的里程碑。

尽管黎曼一生饱受疾病困扰，且在39岁时就去世了，但他的学术贡献已经深深地影响了数学的发展，他提出的黎曼几何理论为描述复杂空间结构，特别是在物理学中的应用提供了理论基础。

黎曼几何的基础

在数学和物理学中，黎曼几何是一种描述曲面和曲线的数学框架，它的特征就是空间中的点，线，面不再像欧几里得空间那样规则和均匀。在黎曼几何中，直线和曲线、平面和曲面的区别开始模糊，这就是我们所说的空间变得“扭曲”。

黎曼几何的基础在于一种特别的概念，被称为“度量张量”。这个张量允许我们在任何点处计算出曲率，并根据这个曲率计算出点和点之间的最短距离，也就是测地线。在欧几里得空间中，测地线就是我们熟悉的直线，但在黎曼几何中，测地线可能是曲线。

这个度量张量的引入，使得黎曼几何具有了描述曲率空间的能力，这种能力在其他的几何体系中是无法比拟的。它可以描述从微小的空间到巨大的宇宙尺度的任何曲率，因此，黎曼几何在物理学中有着广泛的应用，特别是在相对论中。

对于非数学专业的人来说，黎曼几何可能有些难以理解。让我们以一个例子来说明。想象你在地球表面，尽管地球表面看起来是平坦的，但实际上它是曲的，这就是曲率。当你在地球表面行走时，你实际上是在走一条测地线，这条线看起来是直的，但实际上它是弯曲的。

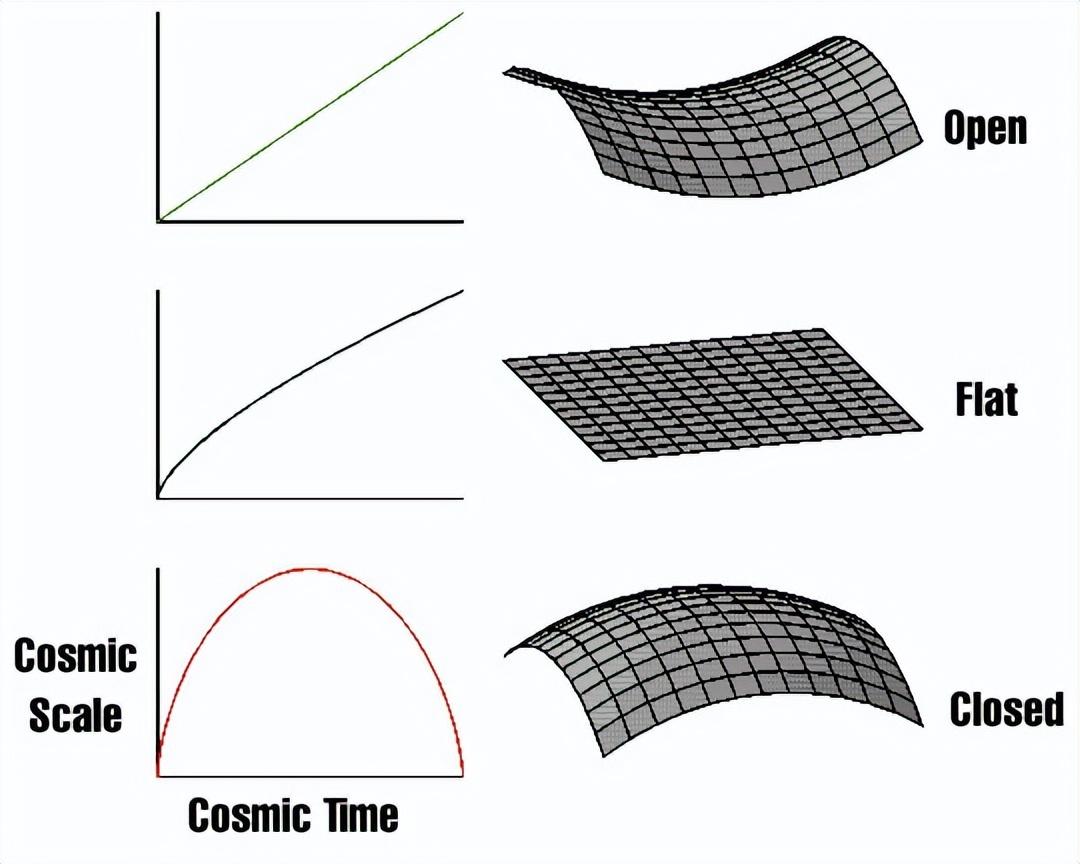
被扭曲的空间——弯曲空间与直平空间的区别

弯曲空间和直平空间的主要区别在于他们的几何特性。在平直空间，或者我们所说的欧几里得空间中，其基本特性遵循我们在日常生活中所熟知的几何规则，例如平行线永不相交，一个角的度数总是180度等等。但在弯曲的空间中，这些“常识”将不再适用。例如，我们可以想象在地球表面（一个弯曲空间）的两条“平行线”（地球的经线），它们在赤道平行，但到达北极和南极时却相交。

而在一个弯曲的空间中，我们会发现，三角形的三个内角之和不再是180度，取决于空间是正曲率还是负曲率，这个和可能大于或者小于180度。同样，圆的周长除以其直径得出的值，也不再是常数π，而是会随着圆的大小变化。

黎曼几何就是对这种弯曲空间的研究，它是一种非欧几里得几何，被广泛用于物理学领域，特别是广义相对论中。在黎曼几何中，空间的性质可以用一种被称为“度量张量”的对象来描述，它可以告诉我们在任何点和方向，空间是如何弯曲的。

总的来说，弯曲空间与直平空间的主要区别在于其几何特性，这些特性影响了我们在空间中测量距离和角度的方式。通过理解这些差异，我们可以更好地理解如何在弯曲的宇宙空间中描述物理现象。

黎曼几何在科学中的应用

黎曼几何的重要性主要体现在其在现代物理学，尤其是广义相对论中的应用。艾因斯坦在提出广义相对论时，就是利用黎曼几何的概念，描述了引力如何通过弯曲时空来产生。

在欧几里得几何中，空间是一个静止不变的舞台，物体沿着直线运动，除非受到外力的影响。然而，在广义相对论中，空间和时间被合并为一个四维的弯曲时空，物体沿着这个时空中的“直线”（在此上下文中，我们通常称之为测地线）运动。

也就是说，在广义相对论中，一个物体在没有外力作用的情况下会沿着时空中的测地线运动，这个测地线是由时空的弯曲决定的。这就是我们通常说的"物体沿着时空的曲率运动"的概念。这种在弯曲的时空中描述物体运动的方式，就是广义相对论的基本原理。

除了广义相对论，黎曼几何还在其他科学领域中发挥了重要作用。例如，在拓扑学，黎曼几何用于研究各种各样的曲面，包括一些在自然界中常见的形状，如星球，甚至更为复杂的结构，如黑洞，虫洞等等。

黎曼几何对我们理解宇宙的影响

黎曼几何是如何影响我们理解和解释宇宙的呢？要回答这个问题，我们需要先了解一下什么是宇宙。简单来说，宇宙是所有存在的事物的总和，包括所有的生命、行星、恒星、星系、星云，甚至包括所有的空间和时间，以及所有的物质和能量。

艾因斯坦的广义相对论是我们理解宇宙的基础，它描述了引力如何通过曲率时空来影响物体的运动。而黎曼几何恰好为描述这种曲率时空提供了工具。在艾因斯坦的广义相对论中，宇宙并非是一个静态的存在，而是一个动态的、时刻在变化的实体。物体的运动和分布能够改变宇宙的结构，而宇宙的结构又反过来决定了物体的运动轨迹。这种相互作用形成了一个动态的、不断演化的宇宙。

黎曼几何也影响了我们对黑洞的理解。在欧几里得空间中，黑洞这样的概念是不存在的。但在黎曼几何中，它们却有了清晰的定义。一个黑洞是空间和时间在强引力下发生极度扭曲的区域，任何接近黑洞的物体甚至光线，都无法逃离其引力，被永久地吸入黑洞。

另外，黎曼几何还影响了我们对宇宙的起源和未来的理解。例如，大爆炸理论就是基于广义相对论和黎曼几何来描述的，它认为宇宙起源于一个热密的状态，并且一直在不断地扩大和演化。在这样的模型中，我们可以探究宇宙的起源，发展，甚至宇宙的命运。

总的来说，黎曼几何不仅为我们提供了描述和理解宇宙的工具，也开拓了我们观察和理解宇宙的新视角。它改变了我们对宇宙的认知，让我们能够在更深更广的层面上理解宇宙的本质和结构。